I am trying to get a grasp on evaluating board positions, for example, for endgame play.
I know that there are counting techniques, and I'd like to see someone demonstrate this with the example shown below.
It's black's turn to play in this position, somewhat early in the game:
I believe that the "correct" sequence is as follows:
And then it is black sente to play elsewhere on the board.
I used to wonder about the real point behind
. If black wants sente, why not take it immediately? That is, don't play and immediately tenuki. Of course, you can then consider the following:Now, white can play on the marked area, but he wouldn't do this, since it would get captured. Therefore, I believe that, after the sequence above, white would tenuki, giving white sente (after b's sente from not playing the original
).So now I can compare what happens if black DID play the original
, but white captures:And again, probably black's sente... So considering these various diagrams, I can make the following intuitive argument:
Quote:
By playing the original , black gets two benefits:
1.) Sente immediately.
2.) Sente again if white decides to capture.
If black omits the original, black gets:
1.) Sente immediately.
2.) Gote if white decides to continue on in the local position.
, black gets two benefits:1.) Sente immediately.
2.) Sente again if white decides to capture.
If black omits the original
, black gets:1.) Sente immediately.
2.) Gote if white decides to continue on in the local position.
By this argument, I can convince myself, "Yes, I should play
"... But this type of reasoning is somewhat of a trial and error approach. It seems sloppy and imprecise. Please illustrate how I can mathematically analyze playing
vs. not playing and taking sente immediately.
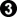connects at (a), B may lose 0.5 points later; but 
sente: the aji of W clamp(b) and W peep(c) -- these are additional reasons for your 
(if W has enough ko threats) --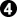
, but has to pull back at (b), losing points:
(W can play 
later, KNOWING about the possibility of 